Whether or not you like math, you’ve probably heard the argument that you should learn math because “you use math every day.” Frankly, I think that this is a stupid argument, and I can’t think of many people who truly use math every day. That’s not to say math is useless. In fact, I want to argue the contrary; while you probably don’t use math every day, you are doing math-adjacent processes every day. In fact, you’ve been doing this since you were a child, but you just haven’t realized it. Let me explain.
I want to introduce you to one of my favorite math problems by way of an example that many of you may have seen before. Along the way, I’ll share some history, show you how an 18th-century mathematician thought about the same problem that you did when you were a child, and hopefully convince you that in a way, we’re all little mathematicians.
The X House
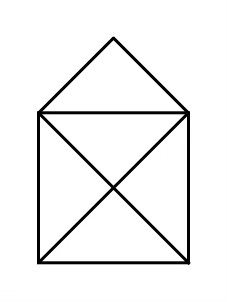
We’re going to start with a game that I first played in elementary school (and maybe many of you did as well). I want you to look at the picture below of this house with an X through it. Your task is to draw this house without lifting your pencil, and without retracing any of the lines. You should start at a corner, and you are allowed to revisit corners (in fact, you’ll have to) but you may not lift your pencil, and you may not draw over a line that you already drew. Once you’ve completed the challenge, make note of where your pencil started and ended.
The Seven Bridges of Königsberg
We’ll revisit the X house later, but I first want to present you with a new problem…a problem that is not so different from the one I just gave you.
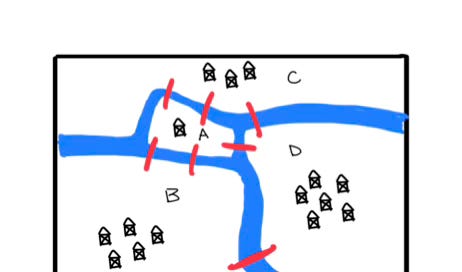
We begin this story in the town of Königsberg in the 18th century. This town, which is now in present-day Russia, sat on both sides of the Pregal River and included two islands in the middle of the river. Seven bridges connected the town. As the story goes, the people of Königsberg spent their time trying to cross all seven. bridges without repeating any of them. Whether or not this part is completely true, I don’t know. But, given that school children spend their time trying to draw houses without picking up their pencils, it’s plausible that 18th-century people liked playing the same game on bridges.
Take a moment to see if you can figure out a way to cross all the bridges exactly once. (Swimming in the river is not a valid loophole!)
Hopefully, you didn’t struggle for too long, because this challenge that you and the people of Königsberg tried to tackle is impossible. How do I know? Well, if you really wanted to torture yourself, you could go figure it out in less than 9,012 tries1, but there is (thankfully) another way.
Euler’s Solution
Leonhard Euler (pronounced oil-er) was a Swiss mathematician born in 1707. He founded the branches of mathematics that are present-day graph theory and topology. The Seven Bridges is thought of as the problem that birthed graph theory.
We’ll first look at Euler’s initial solution to this problem. We will then get into some generalizations that grew from this problem that will help us address the X-house challenge I previously presented.
You might be looking at the seven bridges and thinking to yourself, “I have no idea how I’m supposed to conclude that I can’t cross each bridge exactly once.” But that’s okay, because, at some point, Euler was probably sitting at his desk, looking at his own drawing of the bridges and thinking the same thing. Or really in his case, he was thinking “I have no idea if it’s possible to do this or not.” So at least we’re one step ahead of Euler.
Like any good mathematician, Euler started things simply. Instead of worrying about all seven bridges at once, he started looking for simple patterns that he could generalize2 to help him solve this problem and beyond.
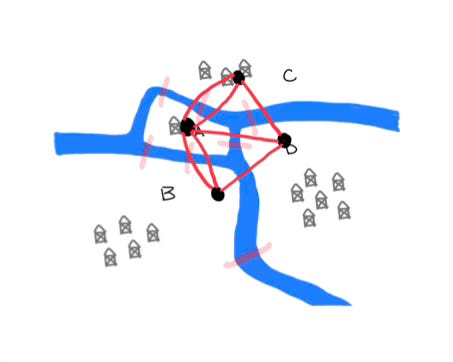
Let’s start by not caring about which bridges we cross, but instead keeping track of what piece of land we come from and what piece we go to. For example, using the labels from the drawing, if I walk from A to B over either bridge, I would document this as “AB”. If I then walk from B to D, I would document this as “BD”. If I wanted to combine the documentation for my two crossings, I could write “ABBD”, but the two B’s in the middle seem rather redundant. So instead, let’s shorten it to “ABD” to signify that I walked from landmass A to B to D, crossing two bridges in the process. If I now walk to C, I would write “ABDC”, and I know I have crossed three bridges total.
Maybe you’re starting to see a pattern. When I have three letters written down, I’ve crossed two bridges, when I have four letters written down, I’ve crossed three bridges. Let’s go further. If I cross another bridge, let’s say I go back to A, I would write “ABDCA”, and these five letters tell me that I have crossed four bridges.
So, if I want to cross exactly seven bridges, I would need to write down eight letters.
We, with the wisdom of Euler, have now reduced this mess of bridges to writing down eight letters. Now, all we need to do is determine if we can create a string of eight letters that would allow us to cross each of the seven bridges exactly once.
This seems both simpler and harder. But let’s start small again.
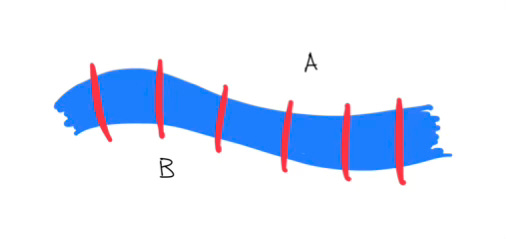
Let’s forget about Königsberg’s setup for a moment and instead imagine we have two pieces of land divided by a river with some bridges between them. The number of these bridges doesn’t matter.
Let’s say I start on B and cross a random bridge to A. Then I would document my travel as “BA”. If I cross another bridge back to B, I would write, “BAB”. If I then cross back to A, I would write “BABA”. So far, I have crossed three bridges, which all touch A. Notice that A is written twice. How many bridges does it take for me to write A three times? I’d have to cross back to B, then cross another bridge back to A, meaning I crossed five bridges to write A three times.
Are you starting to see the pattern?
3 bridges (all touching A) → A is written twice
5 bridges (all touching A) → A is written 3 times
7 bridges (all touching A) → A is written 4 times
To generalize this, if the number of bridges, n, touching A is odd, and I cross all of them, then A will appear (n+1)/2 times3. Note that if we had instead initially started on A and thought about the relationship between bridge crossings and writing B, we would still end with the same result.
This is the key discovery in solving the seven bridges problem:
Given any landmass with n number of bridges touching it, the letter of that landmass must appear (n+1)/2 times to have crossed all of the bridges touching it.
Alright folks, we’ve almost done it. Let’s go back to Königsberg’s seven bridges now, and look at the number of bridges touching each landmass. Using our discovery, let’s figure out how many times each letter should appear.
A has 5 bridges → A should be written 3 times
B has 3 bridges → B should be written 2 times
C has 3 bridges → C should be written 2 times
D has 3 bridges → D should be written 2 times
So based on this, we would need 3 A’s, 2 B’s, 2 C’s, and 2 D’s to fully cross all seven bridges. However, if we add up all these letters, we get nine. Nine letters mean we have crossed eight bridges, not seven.
We have now reached a contradiction. We said that to cross all seven bridges, we must write a sequence of eight letters. However, based on the configuration of bridges and land, we found we would have to cross eight bridges, which is not possible if we want to cross each bridge exactly once4.
In your attempts at crossing all the bridges, you perhaps saw this coming. It’s not too hard to find a route where you have crossed six bridges. However, you then end up stuck. But, if you were allowed to re-cross a bridge, you could probably reach that final, lonely bridge.
Graph Theory
Euler’s solution to the Seven Bridges of Königsberg was just the start of graph theory. Let’s see how this initial work connects to some fundamental ideas of modern-day graph theory.
In Euler’s initial approach, the number of bridges touching a landmass proved to be important. Today, instead of thinking about land and bridges, we use vertices, or nodes, to represent locations, and edges (lines drawn between nodes) to represent the paths that take us between locations (which were bridges in our case). This collection of vertices and edges forms what we call a graph.
In graphs, we call the number of edges touching a vertex (the number of bridges touching the landmass) the degree of the vertex. Graph theory even has a name for crossing every edge exactly once: an Eulerian path (or Eulerian walk).
The degree of each vertex is important in determining if an Eulerian path is possible on a given graph. These generalizations were made by Euler in the same paper that he solved the Seven Bridges problem, but I’m not going to go into detail about how he got there.
For an Eulerian walk to be possible on a graph:
The graph must be connected. This just means that there is a way to travel between any pair of vertices (i.e. an island without bridges is not allowed)
There must be either zero or two vertices of odd degree.
If there are zero vertices of odd degree (i.e. all vertices are even), then it is possible to complete an Eulerian circuit, which means traversing all bridges exactly once and ending where you started.
If there are two vertices of an odd degree, you must start at one of the vertices of an odd degree and end at the other.
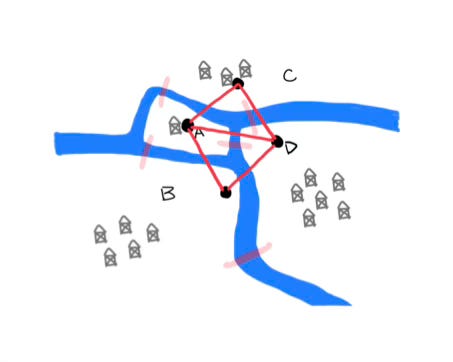
I want to briefly provide some intuition on why we get these restrictions on the degrees of vertices. To do this, let’s consider a version of this problem where an Eulerian path is possible, which historically became possible after two of the bridges were destroyed in WWII.
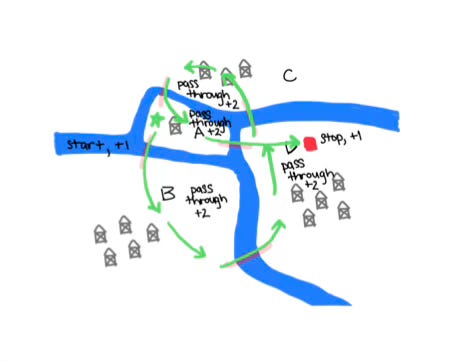
Using Euler’s notation, a valid Eulerian path would be “ABDCAD”. Notice that this Eulerain path, and any that you could come up with, start and end with A and D (or D and A). To understand why, think about the meaning behind the documentation of the path. When a letter is in the middle, it means you’ve arrived at this landmass via a bridge, and left this landmass via a different bridge. So, for every middle landmass visited, there must be at least two bridges touching it, and every time you visit and leave a landmass, you add on another two bridges. On the other hand, when you start or end on a specific landmass, you either start there and leave on one bridge, or cross one bridge to reach the final landmass and stop. If all you do is pass through a landmass and you do not stop or start there, then there must be an even number of bridges touching that landmass. If you start and end on different landmasses, then there must be an odd number of bridges to allow for you starting move across one bridge and your ending move across one bridge. If you want to start and end on the same landmass, then there must be an even number of bridges touching that landmass, since you gain one bridge from starting there and one from stopping there.
Using this logic, see if you can reason your way to why it is impossible to have an Eulerian path if there is only one vertex of odd degree (or landmass with an odd number of bridges). Why is it also impossible to have an Eulerian path with more than two vertices of odd degree? Comment your thoughts below!
Given this set of rules and intuition, return to your X house. You should notice that your drawing started and ended at the two vertices with odd degrees. Given what you know now, it had to be this way.
Who Cares?
If you’re anything like me, then maybe you were easily wowed by the beauty and simplicity of Euler’s solution, or maybe you find drawing pictures without picking up your pencil or retracing lines to be a fun game. But I also imagine some of you are thinking, “Big whoop, who cares about this Euler guy and his graphs?”. This is a valid question.
Graph theory has a number of applications. A popular problem in graph theory is the Traveling Salesman Problem, which asks the following: “Given a list of cities and the distances between them, what is the shortest route to visit each city exactly once?” Or perhaps rephrased for modern times: “Given a list of addresses and the distances between them, what is the shortest route to deliver packages to all these houses?” (Hello, Amazon). You can also check out Colin’s blog post, which uses graph theory to think about planning a public transit system.
Throughout this lesson, we’ve gone from childhood games to 18th-century towns to Amazon deliveries…and somehow the connecting thread in all of this is math. So while the algebra you learned in grade school may not be a tool you’re turning back to in your daily life, I claim that the fundamental approaches in mathematics; pattern finding, generalization of ideas, and deductive reasoning; are all abilities that we naturally use day to day.
For the mathematicians: Given a graph G with adjacency matrix A, the number of walks of length k connecting vertex i to vertex j is (Ak)i,j. The adjacency matrix for the graph made from the proposed seven bridges problem is
using the labeling A through D in the drawing. Then, assuming one tries every walk of length six (since they would likely give up before length seven since one would be forced to repeat an edge), the number of walks of length 6 between all combinations of pairs of vertices, including circuits, is 9,012. However, note that a walk allows for the repetition of vertices and edges. What we want is all trails (a walk with distinct edges) of length six between the vertices, but I am unaware of any nice ways to compute this. Thus 9,012 is most certainly an upper bound for the number of tries.
Higher-level mathematics is all about generalizing and abstracting. We like to think about how far we can stretch our ideas. You’ve seen generalizations before. You know that 2+2=4, and you also know that 2 and 4 are even numbers. But you’ve probably been taught the generalization that the sum of any two even numbers is even. We can generalize this further by saying that the sum of n even numbers is also even. Generalization is critical to mathematics. You can think of it as trying to get the biggest bang for your buck with your ideas.
If this feels like a big jump, that’s okay. This is another example of generalization in mathematics. Instead of continuing to write the pattern we’re seeing (3 bridges → 2 A’s, 5 bridges → 3 A’s, 7 bridges → 4 A’s, etc.), we found a closed formula that can tell us how many times we would write A for any number of bridge crossings, so long as the number of bridges is odd. To understand why this is useful, if not necessary, suppose I have 501 bridges. Do you want to write out the pattern 247 more times? What if I have 1 million bridges? You’d be working all day to incrementally get there. This is where that closed form is really useful.
Maybe this final argument is giving you flashbacks to some TV show or movie with a courtroom scene where the protagonist finally solves the mystery, spotting the flaw in the lies the bad guy was telling. That’s because mathematical proofs use logic and deductive reasoning to draw conclusions, just like law.